为什么 JavaScript 里 0.1+0.2 !== 0.3
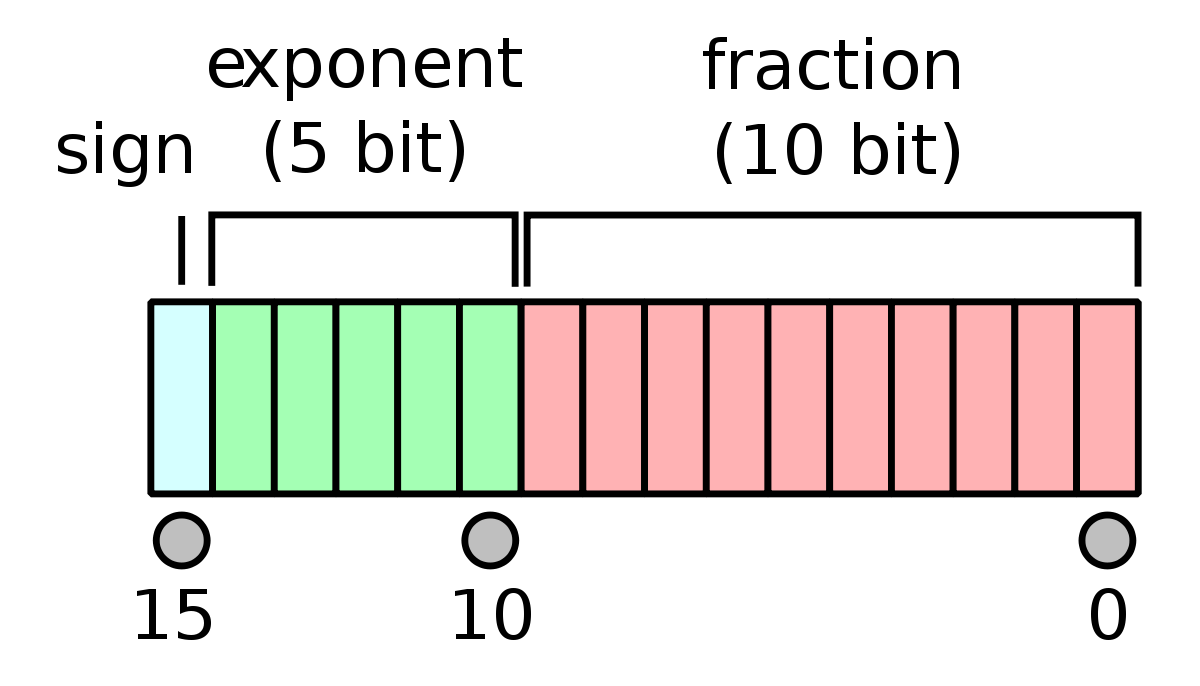
为什么 JavaScript 里 0.1+0.2 !== 0.3?从计算机组成原理角度深挖 JavaScript 浮点数机制。
1 写在前面
以前面试遇到过一个问题:为什么 JavaScript 里 0.1+0.2 !== 0.3。当时我回答了浮点数精度有误差,所以不等于。显然面试官不满意,这不谁都知道吗?
后来看小红书,发现上面也强调过不要进行 0.1+0.2 === 0.3 的判断,但是仅仅提到如下理由:
关于浮点数值计算会产生舍入误差的问题,有一点需要明确:这是使用基于 IEEE754 数值的浮点计算的通病,ECMAScript 并非独此一家;其他使用相同数值格式的语言也存在这个问题。
上面仅仅提到 ECMAScript 使用了基于 IEEE754 标准的浮点数存储机制导致了误差,但是深入 IEEE754 标准,甚至深入计算机层面,又是为什么?作为一个学过《计算机组成原理》的人,我将以计算机的视角,深挖一下答案,希望对你也有所帮助。
2 什么是浮点数?
首先需要知道,计算机中数的表示有定点数和浮点数。
定点数:小数点位置确定。假设 16 位机器字长,可以规定小数点在第 x 位和第 x+1 位之间,例如在第 3 位和第 4 位之间,则表示整数部分有 2 位,小数部分有 13 位(第 1 位表示符号位)。小数点在符号位后面成为小数定点机(这类机器只能表示小数),小数点在末尾成为整数定点机(这类机器只能表示整数)。
浮点数:小数点位置不确定。类似于十进制的科学计数法表示。由 阶数(exponent,含阶码和阶符) 和 尾数(significand,也叫 mantissa,含尾码和尾符) 构成。尾数的位数决定了浮点数的精度,阶数的位数决定了浮点数的范围。
通常定点数由于整数和小数位数固定,因此表示数范围有限,而浮点数通过阶乘,可以让数的表示范围扩大。因此浮点数用途更广。下面这幅图描述了两者的区别:
2.1 浮点数表达式
这里先给出浮点数的表达式:
$$ N = S \times r^j $$
其中 S 为尾码(小数,可正可负,正负由符号位指定),j 为阶码(整数,可正可负,正负由阶符指定),r 为尾数的基值(r 在计算机中通常取 2、4、8、16 等)。
3 浮点数的规格化
3.1 为什么需要规格化?
计算机的浮点数存储时需要进行 规格化(Normalize),而规格化是为了保证精度。
举一个例子,假设一个二进制数:0.000110011001100...(1100 循环),如果不进行规格化,那么尾数部分的 0.0001... 前面的 0 就会浪费尾数空间。可以将尾数左移,移除前面的 0,然后调整阶数,来进行规格化,从而让尾数可以包含更多有效位,从而提高精度。
3.2 规格化形式
浮点数的规格化根据尾数基值 r 不同而不同(以下都指真值表示,补码表示会在下面展开):
- r = 2,尾数最高位为 1
- r = 4,尾数最高两位不全为 0(两位二进制数表示一位四进制数,所以只需前两位不为
00即可) - r = 8,尾数最高三位不全为 0(如上)
- …
3.3 规格化操作
浮点数有两种规格化方式:左规和右规,下面以 r = 2 为例:
- 左规:尾数左移 1 位,阶码减 1
- 右规:尾数右移 1 位,阶码加 1
r = 4 时,尾数移动需要以 2 位为基本单位,以此类推。
由此也可见,r 越大,能表示的浮点数范围越大,同时表示的浮点数精度越低。
4 浮点数在计算机中的运算(加减运算)
了解了浮点数及其规格化,下面我们来看看浮点数在计算机中是如何做加减法运算的。分为如下几个步骤:
- 阶数对齐(对阶)
- 尾数求和
- 规格化处理
- 舍入
- 拓展:浮点数表示范围及溢出判断
以下步骤讲解中的基值 r 均为 2。假设有如下两个值(公式请参考浮点数的表达式):
$$ x = S_x·2^{j_x} \quad y = S_y·2^{j_y} $$
下面只会给出讲解,具体案例会以本文重点的 JavaScript 中 0.1 + 0.2 !== 0.3 进行分析。
首先来看对阶。
4.1 对阶
由于在浮点数的加减法运算中,两个浮点数的阶数不一定相等,而对浮点数进行运算,我们需要保证阶数相等。在调整阶数和尾数,以使得两数阶数相等的过程,就叫做对阶。
4.1.1 求阶差
首先我们需要知道两数阶数差,由于计算机中使用补码进行加减法操作,因此需要注意,其实此处包括后面的尾数求和(或求差)本质上都是使用补码进行。
注意:计算机做减法虽然通常使用补码,但是IEEE 754 标准中规定阶数用移码表示。具体原因及分析后面会给出。
$$ \Delta j = j_x-j_y = \begin{cases} =0 \quad j_x = j_y \quad 已对齐 \\ >0 \quad j_x > j_y \begin{cases} x向y看齐 \quad S_x\leftarrow\Delta j, \quad j_x-\Delta j \\ y向x看齐 \quad S_y\rightarrow\Delta j, \quad j_x+\Delta j \quad √ \end{cases} \\ <0 \quad … \end{cases} $$
4.1.2 对阶原则
我们采用小阶向大阶对齐的原则进行对阶,因为这时尾数移位是右移,即使发生移出丢失,也只会影响数据的精度,而如果发生左移丢失,则会影响数据的大小。
4.2 尾数求和
尾数求和,就是让对阶完成的两个浮点数的尾数部分进行求和操作,这里实际中也会使用补码进行。
4.3 规格化
文章前面简单提到过规格化,但是是建立在真值的基础之上。这里会说明计算机使用浮点数存储尾数时,更实用具体的规格化细节。
我们了解到,规格化是为了最大化利用尾数空间,以获得更高的精度,所以,在尾数求和完成后,新的尾数可能不再满足规格化要求,需要重新进行规格化。
4.3.1 规格化定义
先来复习一下前面提到的规格化形式:
浮点数的规格化根据尾数基值 r 不同而不同(以下都指真值表示):
- r = 2,尾数最高位为 1
- r = 4,尾数最高两位不全为 0(两位二进制数表示一位四进制数,所以只需前两位不为
00即可) - r = 8,尾数最高三位不全为 0(如上)
- …
假设基值 r = 2,结合规格化形式,我们可以对已规格化的尾数 S 给出如下定义:
$$ r = 2 \quad \frac{1}{2} \leq |S| < 1 $$
4.3.2 规格化判断
有了上述定义,尾数大于 0 或小于 0,有如下规格化形式:
| S > 0 | 规格化形式 | S < 0 | 规格化形式 |
|---|---|---|---|
| 真值 | 0.1XX…X | 真值 | -0.1XX…X |
| 原码 | 0.1XX…X | 原码 | 1.1XX…X |
| 补码 | 0.1XX…X | 补码 | 1.0XX…X |
| 反码 | 0.1XX…X | 反码 | 1.0XX…X |
不难看出:
- 对于真值和原码,不论正数、负数,只要第一数位为 1,则为规格化形式
- 对于补码,符号位和第一数位不同,则为规格化形式(计算机可以使用异或电路很轻松地进行判断)
由于计算机使用补码,因此这里只看补码的规格化形式。值得注意的是,我们判断规格化数时,往往使用补码的规格化描述:符号位和第一数位不同来进行判断,而不是使用定义,因为对于补码表示的尾数 S,这里有两个特例:
- 特例一
$$ S = -\frac{1}{2} = -0.100…0 \\ \left[S\right]_原 = 1.100…0 \\ \left[S\right]_补 = 1.100…0 $$
如果按照定义,$S=-\frac{1}{2}$是规格化的数,但是在计算机使用补码对其存储后,按照计算机的异或电路,会认定$\left[-\frac{1}{2}\right]_补$不是规格化的数,因此,如果我们人工分析中遇到了这个特例,需要自己对其进行规格化。
- 特例二
$$ S = -1 \\ \left[S\right]_补 = 1.000…0 $$
上面的情况中,如果按照定义,$S = -1$不是规格化的数,但是 $\left[-1\right]_补$却成为了规格化的数。
注意:小数定点机无法表示 -1 的原码,但是可以表示 -1 的补码。因为原码中 +0 和 -0 是不一样的,而补码中,原码的 -0 被用于编码为 -1。
4.3.3 规格化操作
有了上述的判断标准,我们很容易得出,规格化操作为:
- 左规:在尾数采用补码存储时
- 如果尾数为正数,当尾数第一数位为 0 时,需要进行左规
- 如果尾数为负数,当尾数第一数位为 1 时(由于采用补码存储,因此该位真值一般为 0),需要进行左规。注意: 这里有一个特例,也就是上面提到的特例一,此时应该采用下面提到的右规而不是左规(因为第一数位的 1 实际上也是真值 1,左规移出会导致数据出错)
- 右规:当计算过程中发生尾数溢出($|S| > 1$)时,需要进行右规,防止数据溢出而出错
4.4 舍入
当数据的长度超出了存储该数据的机器字长,我们需要进行舍入。通常在上面提到的对阶和右规过程中,都有可能发生数溢出,此时需要考虑舍入来尽可能保证数据精度。
4.4.1 舍入的几种方法
- 截断法:直接丢弃移出的数
- 0 舍 1 入法:类似于四舍五入,如果丢弃 0 则不管,如果丢弃 1 则在最低位加 1
- 恒置 1 法:不管丢弃的是 0 还是 1,最终保存的结果最低位都保证为 1
- …
在计算机中,还有多种方法可以处理舍入,选择哪种情况具体会考虑数据的精度保证、累积误差以及硬件实现的难易程度等等。下面谈到 IEEE754 标准时,我们还会看到几种舍入方法。
4.5 拓展:浮点数表示范围及溢出判断
上面我们提到移位过程可能造成数的溢出。除了操作时的溢出,还有数存储时的溢出。
如果给定一个浮点数标准(使用补码存储),我们需要判断哪些数会超出存储范围,这个判断也叫做溢出判断。
这里偷一个懒,直接放出刘宏伟老师的计算机组成原理课中的截图:
做一下简单分析,由于机器字长是固定的,因此浮点数能表示的范围和精度也都是有限的,我们便能得到四个关键点:最大(小)的正(负)数,同时得出 5 个区间:
- 比最小负数还小(或比最大正数还大):最小负数,也就是尾数能表示的绝对值最大(-1),阶数也最大时表示的数,如果阶数超过最大阶数,为上溢;正数一边的上溢类似(注意:正数最大无法表示 1,只能为 $1-2^{-n}$)。如果数落在这部分区间,需要进行溢出错误捕获和处理。
- 对应正(负)浮点数:这个区间的浮点数可以被正确存储,不过落在这上面的数都是离散的,并非所有浮点数都能被准确表示,可能会损失一定精度(和舍入规则有关)。
- 下溢区间:下溢区间表示浮点数比最大负数大,却又小于最小正数,通常这个区间的数均会使用 0 来表示。
5 IEEE 754 标准
由于 JavaScript 中浮点数的存储和运算遵循 IEEE 754 标准,因此这里我们先介绍一下这个标准。
IEEE 754 标准是一套关于计算机浮点数的标准,涵盖了浮点数格式、运算、舍入方式以及溢出异常处理等等一系列与浮点数相关的定义和操作,本篇涉及到的主要为浮点数格式和舍入方式。
5.1 主要格式
以下三种为最常见的格式及其不同部分的位数,全部格式请点此查看。
| 符号位 | 阶码 | 尾数 | 总位数 | |
|---|---|---|---|---|
| 短实数(单精度) | 1 | 8 | 23 | 32 |
| 长实数(双精度) | 1 | 11 | 52 | 64 |
| 临时实数 | 1 | 15 | 64 | 80 |
需要注意,由于 IEEE754 标准在尾数中使用了隐含的”1“,所以其实尾数可以表示的位数会多 1 位。
这里简单说一下隐含的”1“,上面规格化判断中提到,规格化的尾数第一位始终为”1“,因此可以将其隐藏,不真正存储在计算机中,而是进行计算时再将其补全。这样做可以将精度扩大 1 位,这里的”1“指的是真值的”1“。
5.2 舍入规则
IEEE 754 标准总共定义了 5 种舍入规则。
前两种为 Roundings to nearest,顾名思义,向最近的有效数舍入,其中 to nearest, ties to even 为二进制浮点数的默认规则,也被推荐作为十进制浮点数的默认规则。与他相关的还有 to nearest, ties to odd,不过没有定义在该标准中。
后三种为 Directed roundings,为直接舍入方法,舍入趋向固定(0、+∞、−∞)。
| Mode / Example Value | +11.5 | +12.5 | −11.5 | −12.5 |
|---|---|---|---|---|
| to nearest, ties to even | +12.0 | +12.0 | −12.0 | −12.0 |
| to nearest, ties away from zero | +12.0 | +13.0 | −12.0 | −13.0 |
| toward 0 | +11.0 | +12.0 | −11.0 | −12.0 |
| toward +∞ | +12.0 | +13.0 | −11.0 | −12.0 |
| toward −∞ | +11.0 | +12.0 | −12.0 | −13.0 |
5.3 在 JavaScript 中的应用
JavaScript 数的存储和操作均使用上面提到的 64 位双精度浮点数标准。
舍入规则使用上面提到的默认规则:Roundings to nearest, ties to even。这里我们主要来讲讲这个规则,规则分为两个部分:
Roundings to nearest
回想一下上面浮点数计算–拓展部分的浮点数表示范围及溢出判断,我们已经知道,并非每一个数都能被精确表示,也就是说我们需要对其进行舍入,使其落在最近的有效数上,而这个有效数,可能比原来的数大,也有可能比原来的数要小,我们需要判断原来的数距离哪一个更近,就选取这个更近的作为舍入后的结果。
ties to even
那么后半句是什么意思?就是如果原来的数距离大的数和小的数距离一样,就选择”偶数“,十进制中的偶数大家都知道,二进制中的偶数,其实就是最低有效位为 0,选择这个数作为舍入后的结果。
举个例子,假设有效位为 4 位,现在有一个数为0.000101,此时其较大的有效数为0.0010,较小的有效数为0.0001,很明显我们需要取0.0001。但如果这个数是0.000111,此时我们则需要取0.0010。
上面的两种情况就是Roundings to nearest。而如果数为0.000110,此时我们参考 ties to even,此时我们需要取0.0010。
这里参考了知乎一个答主的思路,可以很快从二进制上发现规律。舍入时,如果最低有效位后一位为0,则可以知道舍去的数值小于该最低有效位表示数值的一半,此时向下舍入即可(例如上面例子中01小于10)。而如果最低有效位后一位为1,则再往后看,如果有不为0的数,则可以知道舍去的数值大于该最低有效位表示数值的一半,此时向上舍入即可(例如上面例子中11大于10),如果后面数全为0,则根据 ties to even,选择”偶数“即可(例如上面例子中10等于10)。
不知道懂了这个规则的同学,有没有回想起《计算机组成原理》课程里学到过(上面也提到过)的”0 舍 1 入法“。是不是有点像呢?”0 舍“这部分符合 Roundings to nearest, ties to even,而”1 入“则不能无脑做,如果”1 入“前做 ties to even (or odd) 的判断,则”0 舍 1 入法“其实就是 Roundings to nearest, ties to even (or odd),是不是很有趣?
6 JavaScript 中 0.1 + 0.2 的计算
到此为止,我们便掌握了所有的原理,接下来进行实战,看看计算机是怎么对0.1和0.2做加法运算的。
6.1 转换为二进制数
首先需要将0.1和0.2转换为二进制数,对于小数来说,转换为二进制是乘 2 取整操作。我们先计算0.1:
| 运算过程 | 取整 | 小数部分 |
|---|---|---|
| 0.1 * 2 = 0.2 | 0 | 0.2 |
| 0.2 * 2 = 0.4 | 0 | 0.4 |
| 0.4 * 2 = 0.8 | 0 | 0.8 |
| 0.8 * 4 = 1.6 | 1 | 0.6 |
| 0.6 * 2 = 1.2 | 1 | 0.2 |
| … | … | … |
最终可以得到如下结果:
$$ 0.1 = 0.0001100110011001100110011001100….(以1100循环) $$
同理,得出0.2为(为方便展示和比较,也放上0.1):
$$ \begin{aligned} 0.1 = 0.0001&100110011001100110011001100… \\ 0.2 = 0.001&100110011001100110011001100… \end{aligned} $$
6.2 以浮点数形式存储
我们取基值 r = 2,且 IEEE 754 标准中阶数用移码表示(关于移码这里不再赘述,只给出转换后结果),尾数使用补码表示,并进行规格化处理。
简而言之:移码 = 原来的数 + 2^n,n 为数的位数
为了便于显示,我们在以下公式中使用,分割阶数符号位与数值位,使用.分割尾数符号位与数值位,使用:分割阶数和尾数,使用[]表示溢出或隐含的数。
首先需要对尾数进行规格化,由于尾数为正数,且可以隐含第一个”1“,因此尾数表示为:
$$ S(0.1) = 0[1].1001100110011001100110011001100110011001100110011001[1001…](小数点后共52位) \\ S(0.2) = 0[1].1001100110011001100110011001100110011001100110011001[1001…](小数点后共52位) $$
可以看到,上面的数发生了溢出,溢出位为1001...。我们采用默认舍入规则 Roundings to nearest, ties to even,进行处理,得到:
$$ S(0.1) = 0[1].1001100110011001100110011001100110011001100110011010(小数点后共52位) \\ S(0.2) = 0[1].1001100110011001100110011001100110011001100110011010(小数点后共52位) $$
表示完尾数后,再表示阶数(使用移码):
$$ j(0.1) = 0,1111111100(-4) \\ j(0.2) = 0,1111111101(-3) $$
这里顺便说一下使用移码的好处,相信大家也看出来了,使用移码表示后,负数之间的比较也会变得很清晰。
6.3 开始计算
接下来我们开始计算,首先是对阶。
根据小阶向大阶对齐,0.1的阶数+1,尾数进行右移(要注意此时右移第一位补的是隐含的”1“而不是”0“):
$$ \begin{aligned} S(0.1) = 0&.1100110011001100110011001100110011001100110011001101[0] \\ S(0.2) = 0[1]&.1001100110011001100110011001100110011001100110011010 \end{aligned} $$
接下来进行尾数求和:
$$ \begin{aligned} S(0.1) = 0.&1100110011001100110011001100110011001100110011001101[0] \\ S(0.2) = 0[1].&1001100110011001100110011001100110011001100110011010 \\ sum(0.1+0.2) = 0[10].&0110011001100110011001100110011001100110011001100111 \end{aligned} \\ j(sum) = 0,1111111101(-3) $$
sum并非一个规格化的数,我们对其尾数进行规格化:
$$ S(sum) = 0[1].0011001100110011001100110011001100110011001100110011[1] $$
可以看到,规格化后溢出了一个1,继续采用默认规则 Roundings to nearest, ties to even 进行处理,得到:
$$ S(sum) = 0[1].0011001100110011001100110011001100110011001100110100 \\ j(sum) = 0,1111111110(-2) $$
我们来计算一下0.3并对其规格化处理后,得到:
$$ S(0.3) = 0[1].0011001100110011001100110011001100110011001100110011 \\ j(0.3) = 0,1111111110(-2) $$
6.4 比较结果
最后,我们将0.3和sum放一起看看:
$$ \begin{aligned} sum = 0,1111111110:0[1].&0011001100110011001100110011001100110011001100110100 \\ 0.3 = 0,1111111110:0[1].&0011001100110011001100110011001100110011001100110011 \end{aligned} $$
结果相差了$2^{-2}\times2^{-52} = 2^{-54}$!!!
如果再将上面两个二进制数转换成我们熟悉的十次方:
$$ \begin{aligned} sum(0.1 + 0.2) = &0.300000000000000044408920985006… \\ 0.3 = &0.299999999999999988897769753748… \end{aligned} $$
JavaScript 控制台输出:
| |
7 总结
这篇文章的完成历经了很多阶段,重新编写整理了几次。记得第一次写完的时候觉得自己肯定懂了,可是后面翻起来却发现很多地方不知所云,例如对 IEEE754 舍入标准的理解,对隐含”1“操作的理解等等。
由于学习《计算机组成原理》的时候老师只讲了”0 舍 1 入法“等等比较简单易懂的方法,而在实际应用中,例如 IEEE754 标准里,却并没有那么简单,可见学习和实践,是需要相结合起来的。
我仍然不敢说我完全理解了,日后看起来可能还会有不懂的地方,如果大家有疑惑欢迎评论区提出来,一起学习和进步!